| MATLAB Functions | Help Desk |
quad, quad8
Numerical evaluation of integrals
q = quad('fun',a,b)
q = quad('fun',a,b,tol)
q = quad('fun',a,b,tol,trace)
q = quad('fun',a,b,tol,trace,P1,P2,...)
q = quad8(...)
Quadrature is a numerical method of finding the area under the graph of a function, that is, computing a definite integral.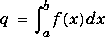
q = quad('fun',a,b)
returns the result of numerically integrating 'fun' between the limits a and b. 'fun' must return a vector of output values when given a vector of input values.
q = quad('fun',a,b,tol)
iterates until the relative error is less than tol. The default value for tol is 1.e-3. Use a two element tolerance vector, tol = [rel_tol abs_tol], to specify a combination of relative and absolute error.
q = quad('fun',a,b,tol,trace)
integrates to a relative error of tol, and for non-zero trace, plots a graph showing the progress of the integration.
q = quad('fun',a,b,tol,trace,P1,P2,...)
P1, P2, ... to be passed directly to the specified function: G = fun(X,P1,P2,...). To use default values for tol or trace, pass in the empty matrix, for example: quad('fun',a,b,[],[],P1).
quad8, a higher-order method, has the same calling sequence as quad.
Integrate the sine function from 0 to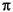 
:
a = quad('sin',0,pi)
a =
2.0000
quad and quad8 implement two different quadrature algorithms. quad implements a low order method using an adaptive recursive Simpson's rule. quad8 implements a higher order method using an adaptive recursive Newton-Cotes 8 panel rule. quad8 is better than quad at handling functions with soft singularities, for example: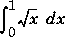
quad and quad8 have recursion level limits of 10 to prevent infinite recursion for a singular integral. Reaching this limit in one of the integration intervals produces the warning message:
Recursion level limit reached in quad. Singularity likely.and sets
q = inf.
Neither quad nor quad8 is set up to handle integrable singularities, such as: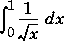
If you need to evaluate an integral with such a singularity, recast the problem by transforming the problem into one in which you can explicitly evaluate the integrable singularities and let quad or quad8 take care of the remainder.
[1] Forsythe, G.E., M.A. Malcolm and C.B. Moler, Computer Methods for Mathematical Computations, Prentice-Hall, 1977.