| MATLAB Functions | Help Desk |
symmmd
Sparse symmetric minimum degree ordering
p = symmmd(S)
p = symmmd(S)
returns a symmetric minimum degree ordering of S. For a symmetric positive definite matrix S, this is a permutation p such that S(p,p) tends to have a sparser Cholesky factor than S. Sometimes symmmd works well for symmetric indefinite matrices too.
The minimum degree ordering is automatically used by \ and / for the solution of symmetric, positive definite, sparse linear systems.
Some options and parameters associated with heuristics in the algorithm can be changed with spparms.
The symmetric minimum degree algorithm is based on the column minimum degree algorithm. In fact, symmmd(A) just creates a nonzero structure K such that K'*K has the same nonzero structure as A and then calls the column minimum degree code for K.
Here is a comparison of reverse Cuthill-McKee and minimum degree on the Bucky ball example mentioned in the symrcm reference page.
B = bucky+4*speye(60);
r = symrcm(B);
p = symmmd(B);
R = B(r,r);
S = B(p,p);
subplot(2,2,1), spy(R), title('B(r,r)')
subplot(2,2,2), spy(S), title('B(s,s)')
subplot(2,2,3), spy(chol(R)), title('chol(B(r,r))')
subplot(2,2,4), spy(chol(S)), title('chol(B(s,s))')
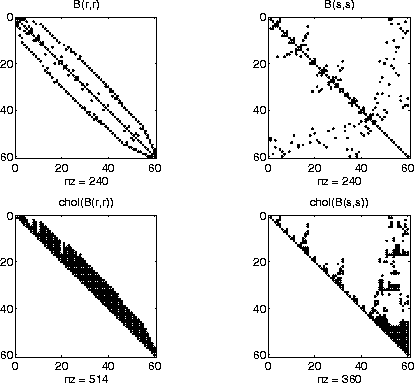Even though this is a very small problem, the behavior of both orderings is typical. RCM produces a matrix with a narrow bandwidth which fills in almost completely during the Cholesky factorization. Minimum degree produces a structure with large blocks of contiguous zeros which do not fill in during the factorization. Consequently, the minimum degree ordering requires less time and storage for the factorization.
colmmd Sparse column minimum degree permutation
colperm Sparse column permutation based on nonzero count
symrcm Sparse reverse Cuthill-McKee ordering