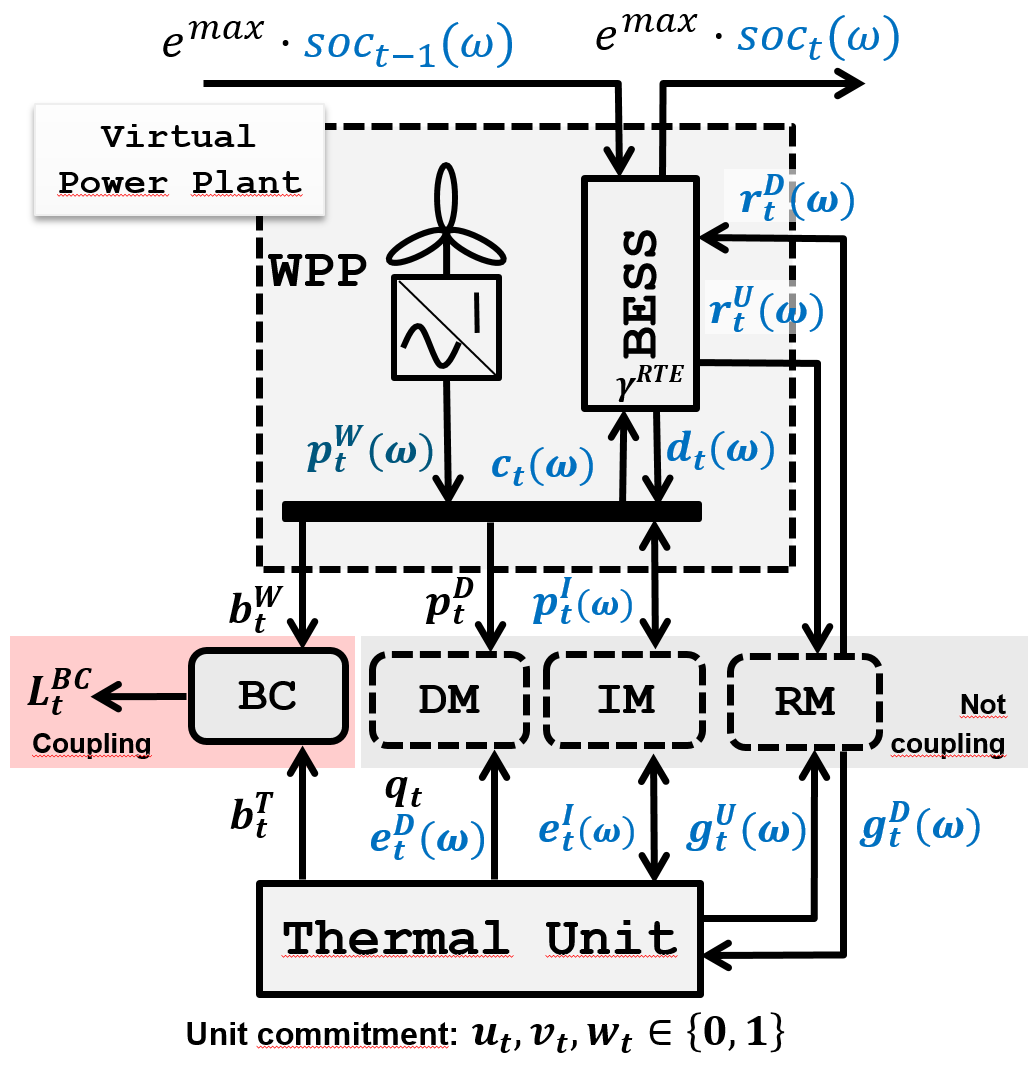
The research project Modelling and Optimization of StruCtured problems and Applications  (MOSCA) of the  GNOM research group of the UPC has been granted by the Agencia Estatal de Investigación (AEI , Government of Spain) in the call PROYECTOS DE GENERACIÓN DE CONOCIMIENTO 2022. The goal of this project is to develop new optimization methods for structured problems, and its application to real cases. I participate as IP, together with professor Jordi Castro, and my specific interest in the project is to work on the formulation and efficient optimization of a multistage stochastic programming model for the optimal participation of energy communities in electricity multi-markets, continuing the research of the ongoing project OptiREC.

Publication Type	Funded research projects
Year of Publication	2023
Authors	Jordi Castro; F.-Javier Heredia; José Antonio Gonzalez; Maria Albareda; Jesica González
Type of participation	Leader (IP)
Duration	09/2023-08/2026
Call	PROYECTOS DE GENERACIÓN DE CONOCIMIENTO 2022
Funding organization	MINISTERIO DE CIENCIA E INNOVACIÓN
Partners	-
Full time researchers	4
Project code	PID2022-139219OB-I00
Key Words	research; energy; optimization; project; competitive; public; AEI; energy communities; stochastic programming
Abstract	The size of current optimization problems (continuous or integer) has grown orders of magnitude in recent years, and, for an efficient solution, their structure needs to be exploited. At the application level, some of the stochastic programming models developed by the group have provided new procedures for the integration of renewable energy in the different electricity markets and have shown, with real data, the superiority of these stochastic methods in comparison to the deterministic alternative. Within the combinatorial optimization context, the group is expert in both, exact and heuristic methods for routing and discrete location problems, with special emphasis to decision problems under uncertainty. The ultimate goal of this project is to develop new optimization methods for structured problems, and its application to real cases.
Export	Tagged XML BibTex