Research
My personal research interests are the evolutive simulation, the use of geographical data in a simulation models, the simulation formalisms and the development of new simulation environments using the more recent technology.
I belong to different groups that helps me and makes my research possible; my department (EIO), the Computing Laboratory of the Barcelona School of Informatics(LCFIB), LOGISIM, LIAM and GORS.
I focus my research in the goal of develops a simulation model of an “evolutive system”, since this objective is quite complex I divide it in different subproblems that can be numbered as:
- Analyze the needed structures to define an evolutive model.
- Define how to use the geographical data in a simulation model.
- Analyze the different formalism used to define simulation models and its applicability to the definition of evolutive models.
- Construct new tools that allow the practical implementation of these goals.
Different projects have been started in order to achieve these goals that can be divided in different areas:
- Environmental simulation.
- Social simulation.
- Tools and methodologies development.
- Sport simulation.
Each one of these area are not independent of the others and represents different aspects of the same objective. In the next section I describe each one of these different areas and the sub goals that they want to achieve.
AREA: Environmental simulation.
During the last years we are involved in the implementation of different models to represent some aspects of the environment, like wildfire simulator (Fonseca et. alt. 2004a, 2004b) slap avalanches simulator (Fonseca and Rodriguez 2007) and black tide simulator among others. Each one of these models has one common denominator; they need geographical structures in order to define the behavior of the model.
The goal of these models is to develop a new paradigm that allows the direct use of geographical data in a simulation model. Up to date methodologies are based on cellular automaton structures (Beneson and Torrens 2004 ), however this approximation lacks in different aspects (Fonseca and Casanovas 2005, Fonseca 2006). We develop a new approximation to this problem, through the m:n-CAk cellular automaton that have some advantages respect the usual cellular automaton (Fonseca and Casanovas 2005, Fonseca 2006). In this area we implement the models using this new structure and we develop the elements that allow its use without any need, from the point of view of the user, of any specific knowledge of simulation. The main goal of this area is to VV&A the slap avalanche model and the black tide model in order to prove that this new methodologies are useful and easy to use.
AREA: Social simulation
Since not all the behaviors are as “simple” as the wildfire spread, we need to develop new structures to allow modeling, for instance, a mammal behavior. In this area the final goal is to allow the representation of the human behavior. The methodologies used in this area are based in MAS systems. In our approach we integrate the MAS systems with the developed methodologies of the environmental simulation, allowing a complete definition of the environment and allowing the interaction between different kinds of models.
Since in a social model the complexity of the behavior can be big, we investigate the formalism needed in order to define unambiguously this behavior, without complicate the understanding of the model for personnel that usually are not used with a mathematical formalizations. In this research we are developing some generic structures that can be used to define intelligent agents in order to simplify the model definition.
Two main projects are related to this area, the simulation of the Tribul behavior (a plant) in collaboration with the Department of Agri Food Engineering and Biotechnology (DEAB) bellowing to Polytechnic University of Catalonia (UPC), and the simulation of the behavior of small societies, like the Lenuria project, that has the main objective of simulate the medieval Girona.
AREA: Tools and methodologies
As we see in the previous area the methodologies are important since allows a complete communication between the different actors defining the project. Different formalism exists to define a simulation model, Petri nets, DEVS, SDL among others, however only a few tools allow a complete simulation from model formalization.
In this area we are developing a new tool, named SDLPS, from the experience obtained by our group from the development of commercial simulation tools, like LeanSim or VRABox. This system allows the simulation of a model formalized using SDL formalism. Since we develop a method to transform SDL to DEVS and vice versa (Fonseca and Casanovas 2005, 2006) the final objective of this tool is to allow to run a simulation formalized first in SDL,next in DEVS and finally in Petri Nets, since a mechanism to transform a formalism from DEVS to Petri nets exists.
SDLPS allows a distributed execution of a simulation model, without the need of parallelize the model, since SDL formalism take care of this problem. First steps of the development of this tool have been achieved (Fonseca 2008).And some projects, using this tool and the methodologies exposed in the previous areas, started.
AREA: Sport simulation
This area represents a specific use of the knowledge obtained from the other areas. The problem is to simulate the behavior of an athlete in a specific competition. The main goal is to optimize his/her training and give information to the trainer to select the best “player” for a specific competition.
As we see the final objective is double. From the point of view of the trainer, to obtain an expert system that helps to determine what are the best athlete for an specific competition depending on different factors (for instance in a soccer match what are the best players depending on its physical condition and the scheduler, or in a marathon race who can be the athlete that must run the race, to allow the club to achieve more points during the different athletic courses of the schedule).
From the point of view of the athlete the main objective is to improve the training and to help avoiding problems related to the overtraining or injuries, helping the trainer deciding the microcycles, mesocycles and macrocycles of a training season for a specific athlete, depending of course on his/her personal objectives.
To model this system is needed to use GIS, complex behavior defining the athletes, and other methodologies of the O.R.
Concluding remarks
All this areas are widely connected, because in order to step forward in each one of them is needed to step forward in the others. However, the separation in different areas allows defining more specific goals that are more suitable that the final objective. Also the main objective of each one of the different areas is very interesting by itself.
References:
Benenson, Itzhak; Torrens, Paul M. 2004. Geosimulation: automata-based modeling of urban phenomena. Wiley.
Fonseca , Pau; Casanovas, Josep; Montero, Jordi. 2004. GIS and simulation system integration in a virtual reality environment. Proceedings of GISRUK 2004.Pages: 403-408 Editors:: University of East Anglia (pdf) (poster) First prize poster winners in the 2004 conference.
Fonseca i Casas, Pau; Casanovas, Josep; Montero, Jordi. 2004 A cellular automata and intelligent agents use to model natural disasters with discrete simulation Environmental Modelling and Simulation 2004. EMS 2004 ref: 0-88986-443-8 pages: 96-101. Editor: Ubertini
Fonseca, Pau. Casanovas, Josep. Simplifying Gis Data Use Inside Discrete Event Simulation Model Through m:n-ac Cellular Automaton. A: Procediings. Chiara BRIANCO, Claudia FRYDMAN, Antonio GUASCH, Miquel Angel PIERA, 2005, p. 7-15.
Fonseca, Pau. Casanovas, Josep. Using SDL diagrams in a DEVS specification. A: MSO 2005. IASTED G. Tonella, 2005, p. na-na.
Fonseca, Pau. Vectorial Data Use in a m:n-AC Cellular automaton. A: Proceedings of the GIS Reseach UK 14th Annual Conference. Gary Priestnall and Paul Aplin, 2006, p. 350-356.
Fonseca, Pau. Casanovas, Josep. Transforming SDL Diagrams in a DEVS Specification, Modelling, Simulation and Optimization. A: Procediings MSO 2006. H. Nyongesa , 2006, p. ---.
Fonseca, Pau. Rodríguez, Santiago. Using GIS data in a m:n-ACk cellular automaton to perform an avalanche simulation. A: Proceedings of the Geographical Information Science Research UK Conference. Adam C. Winstanley, 2007, p. 45-50.
Fonseca, Pau. SDL Distributed Simulator. Proceedings of the Winter Simulation Conference 2008. Poster session.
EVOSim
What is an evolutionary system?
A system is a set of entities – for instance, people or machines – that interact with a common objective (Law and Kelton 1991). This objective can be implicit or explicit. Therefore, the system presents change resistance.
In practice, the definition of what is and is not a system depends on the object of study. To help in the study of the system, a system state is defined. This set of variables describes the system at a specific instant. This description tries to answer the question that motivates the construction of the model. By analyzing the system state, the first division can be established, depending on the evolution of the variables. The modification can be continuous or discrete[1].
Systems can be classified based on whether they modify their behavior during the simulation depending on the system state. Systems that modify their behavior are called evolutionary systems, the systems that learn. Those that do not learn are called interactive systems[2] (Henning 2001), where the results are obtained by the effect of the interaction between the different elements of the model.
The use of evolutionary methods rather than classical interactive methods is determined by the elements quoted below (Henning 2001):
“If the characteristics of entities do not change, or stay in a variability range which is controlled by the factors internal to the entities (control structures, information carriers like genes in biological entities) but not a selecting influence, there is no evolution in the Darwinian sense of the term and ’interactionist’ models should suffice to describe the history of the system.” Examples of this kind of system include industrial systems, in which the variability of the different variables of the model elements (machines) is always within a specific range. Biological models are another example: the simulation time is shorter than the time required to change the behavior of the elements (study of mammals’ population dynamics).
“If the characteristics of the entities change, the characteristics are under some kind of selection and generations of characteristics are connected by tradition, i.e. there exists some form of heredity, we can meaningfully speak of and borrow from evolutionary models. These models will sometimes be confined to the biological, Neo-Darwinian type though.” Tradition appears in these models, which allows new characteristics, properties and behaviors to appear. Tradition allows the change, and selection motivates the change. Systems of this kind are able to learn.
A third case can exist. If the characteristics change but tradition is unable to create new values, the inheritance mechanism does not exist. This case is open to discussion (Henning 2001).
Systems can be classified based on time, whether the system is dynamic or static, and whether the behavior of the model elements changes. Table 1 (Henning 2001) shows how systems can be classified based on the variable pairs static/dynamic systems and interactive/evolutionary systems.
|
|
Static systems
|
Dynamic systems
|
|
Interactive
|
Static interactions. The only changes are in the composition. For instance, systems that are not modified over time. Through Monte Carlo simulations, an approximate value can be obtained.[3]
|
System interaction. Changes in the interactions between the different model components. For instance, an industrial plant.
|
|
Evolutionary
|
Evolutionary selection. Random acquisition of variations that change the composition of types.
|
Evolutionary system feedback that influences the supply of variation and the speed of evolution. Changes in type depend on the history of the system. For instance, the evolution of a society or wildfire with the interaction of an extinction model.
|
Table 1: System classification.
The classification of a system as one type or another depends on the temporal scope of the problem being studied. For instance, if the lifetime of the simulation model is short and the feedback from the modifications to the behavior of the entities has no effect on the model, then an interactive model should suffice. Other more complex classifications can be done, for instance Marín and Mehandjiev (2006) proposes a classification for AMAS[4] based on its definition and the relation with the environment: “MAS situated in an open environment and capable to self-modify its structure and internal organization by varying its elements’ interactions according to environmental changes”.
|
|
Enviroment
|
||
|
|
Relation
with the environment |
Discrete
|
Continuous
|
|
Static
|
Strong
|
Automaton
|
Control system
|
|
Weak
|
Semi-Isolated Evolution
|
||
|
Dynamic
|
Weak
|
Complex Interactions
|
|
|
Strong
|
Ecosystem
|
||
Table 2: AMAS System classification (Marín and Mehandjiev 2006)
Table 2 shows that depending on the relation with the environment of the systems, these can be classified in five different categories: Automaton, Control System, Semi-Isolated Evolution, Complex Interactions, and Ecosystem”. The emergent behavior that appears[5], caused by the selection rule, can be classified in two main classes, depending on the interaction of the model individual elements:
- Collaboration
- Competition
With these two types of interaction and the possibility of a system being either interactive or evolutionary, entities can present entirely different behaviors.
Table 3 shows the possible evolution of a model (Henning 2001).
|
|
Interactive systems
|
Evolutionary systems
|
|
Competition
|
Differentiation
|
Desestabilization
|
|
Collaboration
|
Interactive emergence
|
Combinatory emergence
|
Table 3: Evolution due to individual behaviors.
In an interactive system, where the various elements do not evolve, differentiation appears if competition between the elements causes them to separate and become differentiated. Destabilization appears if the elements evolve or if they can develop their own strategies or behaviors in order to beat their adversaries. However, if the elements collaborate, a global behavior emerges.
The next section discusses evolutionary systems and studies the tradition mechanism that makes evolution possible. There are two main families of systems, depending on whether tradition exists: neo-Darwinist systems and evolutionary systems.
Neo-Darwinist systems are based on the assumption that mutations, or changes in the system rules, are random and not directed at any goal. Evolutionary systems are based on the assumption that changes are not random – even if they are not directed at a specific goal. In evolutionary systems, changes are directed by the existence of a structure – the structure of the organisms – and the limits it places on changes. For a more complete view of these concepts, see Riedl (1975) and Maynard and Szathmary (1995).
To avoid this dilemma, the concept of mutation can be distinguished from the changes that result from mutation. Mutation can be random and need not favor one specific direction. Hence, only a small proportion of these mutations can be applied to an organism and modify its behavior in the long term.
[1] A model can represent a system at a specific time (a static representation). The introduction describes a classification based on the existence of time evolution in a system: static systems and dynamic systems. Systems can also be classified based on whether random variables are used in the simulation model. Models that use random variables are called random models. Models without random variables are considered deterministic models.
[2] “The interest of the interactionist perspective is usually focusing on the emergence of aggregated patterns of behavior and its effect in larger systems.” (Henning 2001).
[3] One example of an interactive static system is pi-calculus using Monte Carlo simulations. In this example, there is no time but the composition is modified during the simulation because the procedure produces an increasing number of points (with more points, the value is closer to the value of pi).
[4] Adaptative multiagent-systems. adaptive agent is that who has knowledge about its own structure and evolutionary capacities (i.e. meta-knowledge), so that it can dynamically modify its behavior by changing its own structure (Guessoum 2004). These systems are in the Evolutionary section of the Henning classification.
[5] According (Marín and Mehandjiev 2006) the two kind of systems that allows the emergence of a behavior are Ecosystems and Complex-Interactions.
References:
Guessoum, Z. 2004 Adaptive agents and multiagent systems. IEEE Distributed Systems Online 5(7) http://dsonline.computer.org/ (accessed 15 January 2007).
Henning Reschke, Carl. 2001 Evolutionary perspectives on simulations of social systems, Journal of Artificial Societies and Social Simulation, Vol. 4, No. 4. [e-journal] http://jasss.soc.surrey.ac.uk/4/4/8.html (accessed 12 January 2006).
Law, A. M.; Kelton, W. D. 1991. Simulation modeling and analysis. McGraw-Hill.
Marín, César A.; Mehandjiev, Nikolay. 2006, A Classification Framework of Adaptation in Multi-Agent Systems, Lecture Notes in Computer Science, Cooperative Information Agents X, pp 198-212, Springer Berlin / Heidelberg, ISBN: 978-3-540-38569-1, http://www.springerlink.com/content/aq84716t957ujt11 (accessed 16 January 2007)
Riedl, R. 1975. Die Ordnung des Lebendigen. Systembedingungen der Evolution. Paperback ed. Munich: Piper.
Werner, Roland. 2000. Structure, flow, change: Towards a social systems simulation methodology. Social Systems Simulation Group. San Diego State University.
GEOSim
In a GIS, data can be represented in two main different formats (Korte 2001)[1]. The first format, raster, defines a matrix of points. In each cell, a numerical code is defined. This code, usually a real number, can represent different kinds of geographical data, such as elevations and terrain properties. The second format, vector, defines a set of vectors that represent geographical data. This format comes closer to the natural representation of geographical data on paper. Figure 1 explains how reality is represented using these two alternatives. Vector data is shown on the left and raster data is shown on the right.
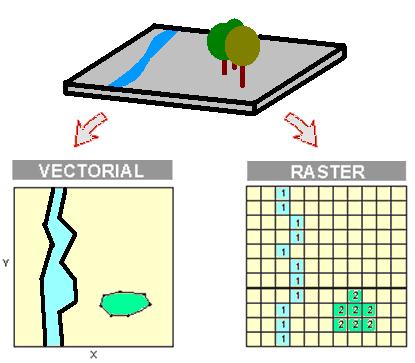
Figure 1: Raster and vector layers of a GIS.
Using a cellular automata to use GIS data in a model is not a new concept. Studies in this area can be reviewed in Benenson and Torrens (2004) and Fonseca and Casanovas (2004).
The nexts sections describe the different elements needed for this use and the data used in the simulation engine. A wildfire model using this approach is presented as an example. This example can be reviewed in the projects section and is based on Rothermel's mathematical model (Rothermel 1972, 1983).
GIS layers
This section classify the different structures used as layers in the simulation model in this study (Fonseca and Casanovas et al. 2004).
- 2DLayers (vector layers): These layers represent the common geography layers of a GIS, such as points, polylines, text and lines. Added to the virtual model, these elements usually represent information for the observer but not for the simulation model. They usually do not have specific behaviors. However, simple behaviors may be defined for the entire layer.
- 3DLayers (raster layers): These layers are used to represent fixed populations of elements such as forests or cities (each tree has its own location in a DEM). The restriction is that all elements must have the same virtual representation and behavior. A raster file is used to establish the exact position of each object. This file contains a matrix of data that shows the position of each element. There are two different kinds of raster file. The first kind uses a binary data structure, which only represents the absence or presence of the object represented by the 3DLayer in a given position; in this case, the object is located just over the DEM. The second kind of file uses a data matrix that represents the position of the object in the Y-axis position (elevation). Obviously, in this second approach, the no-data value shows that there is no element in this position[3]. In the wildfire sample, we use
- 3DLayers to represent the forest trees that can be burned by the fire. The simulator can interact with these elements individually in order to simulate wildfire propagation.
- Objects: The limitation of using layers is that all elements of a given layer must have the same behavior. If we need to represent an element with specific or individual behavior, we must use “Objects” (2DObjects or 3DObjects).
- 2DObjects: These objects represent lines, polylines, texts and points with individual behavior – for instance, a point with a touch sensor that shows certain information.
- 3DObjects: These are virtual objects that are not associated with any layer. They can have unique behavior represented by a script or program connected to the world (through EAI[4] for instance).
Routes: Routes define the movements of 3DObjects through the virtual landscape. These objects may or may not be part of a 3DLayer. Routes can also be defined by the simulator. They allow the different elements to move through the landscape in accordance with the simulator’s logic.
Some 3DObjects are integrated with a GPS. As a result, simulators can implement training systems. Elements can be located in the real world and be placed in the model, and hence the implications of their locations or actions can be determined.
| Layer | GPS integration |
| DEM | Georeferenced |
| 2DLayers | Georeferenced |
|
3DLayers
|
Georeferenced |
| Routes | Track points |
| 2DObjects | Waypoints |
| 3DObjects | Waypoints |
Table 1: Integration of layers with GPS.
Each of these different elements can be used in a simulation model. For instance, 3D layers can represent forests. Each 3D layer can represent a specific kind of vegetation. 2D layers can represent rivers or territorial divisions, or the wind direction in a wildfire-propagation model.
Once all the needed data is defined, some kind of interface must be defined in order to use it in the simulation model.
GIS, virtual reality and simulation
Outdoor simulation models may require a huge set of GIS data. Consequently, an interface must be established between this data and the simulation model that allows the data to be represented and used in the model.
Virtual reality helps represent landscapes, theoretically more realistically than any other technology. It helps represent not only visual landscapes but also computer data. Virtual reality stores the physical structures of a landscape and the simulator uses those physical structures to enable interaction with landscape elements. This also makes it possible to perform active queries on the outdoor simulation model.
In recent years, the main providers of GIS tools have developed several techniques for improving data representation, especially in 3D. Some only show a static 3D view, while others allow a 3D view with navigation, free flying or recorded animation over the data representation. In our approach, we use virtual reality techniques (using VRML 2.0 as the standard representation language; see Andrea L. Ames (2000)) to enable powerful interaction with the various model elements. Obviously, the GIS data must be prepared and converted to VRML and sensors, scripts for dynamic behavior and other functionalities based on External Authoring Interface (EAI) must be added.
In our wildfire implementation, for instance, the GIS stores the data that represents the landscape – basically the DEM model and the vegetation structure – in virtual reality format. Through this representation, the simulation model knows the configuration of the terrain and can facilitate interaction between it and the various model elements. The difference between a virtual DEM representation and a simple DEM is the interaction. A virtual DEM representation enables interaction between one or more users and the landscape. These users can navigate the virtual landscape, respecting certain rules such as collision detection and gravity, which can be defined in the virtual representation of a DEM but are never defined in a DEM. These rules are useful because the simulator needs not only the structure of the landscape but also the most important rules applied to it (gravity, collision detection, lights, etc.). These rules help define the relationship between the simulation model and the landscape.
Virtual landscape generation
Data can be converted from GIS to virtual reality using specific tools such as VirtualLands© (Figure 2). This tool works with several of the most common GIS file formats (shape, raster, DEM, etc.) and converts them to analogous layers in VRML, exports data to LeanSim® file formats and builds a VRML file that contains all the information needed to simulate or query the GIS data in a 3D view.
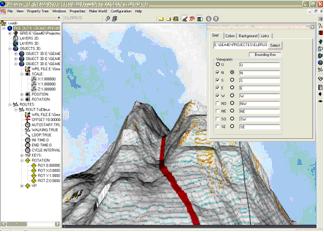
Figure 2: VirtualLands©.
References:
Ames, Andrea L.; Nadeau, David R.; Moreland, John L. 2000. VRML 2.0 Sourcebook, 2E. 688.
Benenson, Itzhak; Torrens, Paul M. 2004. Geosimulation: automata-based modeling of urban phenomena. Wiley.
Fonseca i Casas, Pau; Casanovas, Josep; Montero, Jordi. 2004. GIS and simulation system integration in a virtual reality environment. Proceedings of GISRUK 2004.
Malczewski, Jacek. 1999, GIS and Multicriteria Decision Analysis, John Wiley and Sons, 408 pages, ISBN 0471329444
Rothermel, R. 1972. A mathematical model for predicting fire spread in wildland fuels. Research Paper INT115. Ogden, UT: US Department of Agriculture, Forest Service, Intermountain Forest and Range Experiment Station.
Rothermel, R. C. 1983. How to predict the spread and intensity of forest and range fires. USDA Forest Service Research Paper, INT115. US Department of Agriculture, Forest Service, Intermountain Forest and Range Experiment Station.
Formalization
The growing complexity of simulation models requires a formal system that helps in model specification. This is truer still when the different individuals working to build the model come from different areas, and especially if the model is evolutionary. An example would be a social model or an economic model with engineers, economists, sociologists, psychologists and other researchers working on it. This factor, detailed in Werner and Werner (1972), makes it necessary to establish a common mechanism to help in the definition of elements’ behavior. Nevertheless, due to the diversity of the various elements of the model (some of which could be considered submodels), some formalisms are easier to use than others. The relative speed of the different submodels can be a good indicator for determining what is best in each case.
Mechanisms to transform models between different formalisms can therefore be useful. They allow the use of different formalisms depending on the submodel and help integrate the specification of the entire model through the formalism transformation.
In his paper “DEVS as a common denominator for multi-formalism hybrid systems modeling” (Vangheluwe 2000) Hans L. M. Vangheluwe clearly expresses the need to establish mechanisms for working with models specified by different formalisms. He explains three of the main mechanisms for doing this:
- Meta-formalism: A formalism that incorporates the different formalisms of the various submodels that make up the system.
- Common formalism: A mechanism that converts all formalisms to a common formalism.
- Co-simulation: Independent simulators that work together.
The specification formalism must be easy and clear, so that people who are not used to working with formalisms can quickly understand the model. The formalism must also be powerful, so that the complexity of the model can be represented.
It is difficult to determine if one formalism is simpler than another, because everyone has a personal preference. This chapter therefore presents a theoretical connection between two of the most widely used specification formalisms: DEVS and SDL.
DEVS, developed by mathematician Bernard Zeigler in the 1970s, is one of the most powerful formalisms for the specification of discrete event systems (DES). It is based on systems theory, which makes it universal. Hence, all other formalisms can be represented through DEVS models (Zeigler and Vahie 1993). That is, models represented by a Petri net or by differential equations can be represented in a DEVS model. Hybrid models are more complicated, but can also be represented by DEVS.
In his paper “Structure, flow, change: toward a social systems simulation methodology” (Werner 2000), Ronald Werner proposed the creation of an environment to describe sociology models: “The modeling environment consists of three structural elements: (1) The social system states are symbolized by circles. (2) The social processes are symbolized by rectangles. (3) The direction of flow is symbolized by directional arrows.”
This work clearly expresses the need for a graphical representation of model structure. Werner's model representation environment has similarities with the SDL formalism, which leads us to believe that it could be a good graphical representation formalism for DEVS in the social sciences and, more generally, in evolutionary models.
References:
Werner, Roland; Werner, Joan T. 1972. A pragmatic approach to social systems modeling and simulation. Social Systems Simulation Group, San Diego State University.
Werner, Roland. 2000. Structure, flow, change: Towards a social systems simulation methodology. Social Systems Simulation Group. San Diego State University.
Zeigler, Bernard P.; Vahie, Sankait. 1993. DEVS formalism and methodology: unity of conception/diversity of application, in the proceedings of the 25th Winter Simulation Conference. pp. 573-579. 12-15 December 1993. Los Angeles, California, United States (accessed 17 January 2005).
Simulation models
Here you can find different simulation models developed using some of our tools, or from scratch.
Avalanche
The simulation of a snow slap avalanche phenomena using GISSim techniques for the information representation and EVOSim techniques for the propagation.
In the next figure a representation of an avalanche using the simulation model is shown.

The validation and the verification of the model is performed thanks the information provided by the IGC.
Thesis related.
There are 2 thesis related with this project here.
Publications related.
If you have a question about the publications please feel free to ask me anything.
GISRUK 2007
11-13th April 2007. NUI Maynooth, (Ireland) |
Computers, Environment and Urban Systems 2010A novel model to predict a slab avalanche configuration using m:n-CAk cellular automata http://www.elsevier.com/wps/find/journaldescription.cws_home/304/description#description 23 August 2010 |
GISRUK 2007 Presentation
Using GIS data in a m:nACk cellular automata to perform an avalanche
GISRUK 2007
Index
• • • • • • Avalanche problem Cellular automata m:n-ACk Avalanche model Results Conclusions
GISRUK 2007
2
Avalanche
Two main types of snow avalanche: • Loose-snow avalanche originates at a point and propagates downhill by successively dislodging increasing numbers of poorly cohering snow grains, typically gaining width as movement continues down slope. • Slab avalanche, occurs when a distinct cohesive snow layer breaks away as a unit and slides because it is poorly Cellular automata – the snow or ground Avalanche – anchored to m:n-Ack – Avalanche model – Results
– Conclusions
GISRUK 2007 3
Avalanche fatalities in IKAR Countries
Avalanche – Cellular automata – m:n-Ack – Avalanche model – Results – Conclusions GISRUK 2007 4
Cellular automata
Avalanche – Cellular automata – m:n-Ack – Avalanche model – Results – Conclusions GISRUK 2007 5
Game of life
• The Game of Life is a cellular automaton devised by the British mathematician John Horton Conway in 1970. It is the best-known example of a cellular automaton. • Glider gun and
GISRUK 2007 6
m:n-ACk
A multi n dimensional cellular automaton is a cellular automaton generalization composed by m layers with n dimensions each one. The representation is: • m:n-ACk Where • m: is the automaton number of layers. • n: is the different layers dimension. • Avalanche – Cellular automata – m:n-Ack – Avalanche model – Results k: is the number of main layers (1 by
– Conclusions
GISRUK 2007 7
m:n-ACk
• Defined over the mathematical topology concept. • 1:n-AC 1 is the common cellular automata if the topology used is the discrete topology defined over N or Z. • The implementation, as is usual, can be a matrix.
GISRUK 2007 8
State of the automata
• Em[x1,..,xn], layer m state in x1,..,xn position
– Em is a function describing cell state in position x1,..,xn of layer m.
• EG[x1,..,xn], automata status in x1,..,xn position.
– EG returns automata global state in position georeferenced by coordinates x1,..,xn. Avalanche – Cellular automata – m:n-Ack – Avalanche model – Results
– Conclusions
GISRUK 2007 9
Evolution Function m
• Function defined for the layer m to modify its state through the state of others layers using combination function Ψ, and vicinity and nucleus functions.
Avalanche – Cellular automata – m:n-Ack – Avalanche model – Results – Conclusions GISRUK 2007 10
Avalanche Model data
GISRUK 2007
11
Avalanche Model
• 6+N:2-AC4+N on Z2
Avalanche – Cellular automata – m:n-Ack – Avalanche model – Results – Conclusions GISRUK 2007 12
Vicinity and nucleus function
• Vicinity function: vn(x1,x1) = {(x11,x2-1), (x1-1,x2), (x1-1,x2+1), (x1,x2-1), (x1,x2), (x1,x2+1), (x1+1,x2-1), (x1+1,x2), (x1+1,x2+1)} • Nucleus function: nc(x1,x1)= {(x1,x1)}
Avalanche – Cellular automata – m:n-Ack – Avalanche model – Results – Conclusions GISRUK 2007 13
Evolution functions
• E2[i]: Thickness of the snow. The function that rules this layer is “Modify information(p)” • E4[i]: Density, compactness of the snow, in our case is 0.5 (Mears 1976). • E6[i]: State of the snow. The function is defined in the next diagrams. • EN[i]: Obstacles. The function that
GISRUK 2007
14
SDL formalism
• Object-oriented, formal language defined by The International Telecommunications Union as recommendation Z.100. • Intended for the specification of complex, event-driven, real-time, and interactive applications involving many concurrent activities that communicate using discrete signals.
Avalanche – Cellular automata – m:n-Ack – Avalanche model – Results – Conclusions GISRUK 2007 15
Moore neighbourhood
Avalanche – Cellular automata – m:n-Ack – Avalanche model – Results – Conclusions GISRUK 2007 16
Λ:state of the snow
Avalanche – Cellular automata – m:n-Ack – Avalanche model – Results – Conclusions GISRUK 2007 17
Empty process
GISRUK 2007
18
Results
Avalanche – Cellular automata – m:n-Ack – Avalanche model – Results – Conclusions GISRUK 2007 19
Results
Avalanche – Cellular automata – m:n-Ack – Avalanche model – Results – Conclusions GISRUK 2007 20
Conclusions
• An application to represent in virtual reality format the avalanche phenomena using GIS data thought the m:n-CAk cellular automaton is presented. • The comparison of the output data with studied phenomena shows promising results. • The structure in layers simplify the calculus of the evolution functions, allowing an easier implementation of the model, and a clear specification. • Avalanche –represents all m:n-Ack – Avalanche model – Results Layers Cellular automata – the model variables,
– Conclusions
GISRUK 2007 21
Thanks!
Pau Fonseca i Casas pau@fib.upc.edu
Technical University of Catalonia Barcelona School of Informatics Computing laboratory Barcelona Jordi Girona 1-3 (+34)93401773
GISRUK 2007 22
Static process
GISRUK 2007
23
Dynamic process
GISRUK 2007
24
Evolution function
• The increment in the force is used in the next expression to determine if the snow continues its movement to other cell, or stops its movement, if the force is equal to zero.
GISRUK 2007
25
Evolution function
• Where • IFi,t=Impulse force, depends on the quantity and quality of the snow, and the slope. • SFFi,t= Sliding friction force between the avalanche and the underlying snow or ground. • IFFi,t= Internal dynamic shear resistance due to collisions and momentum exchange between particles and blocks of snow, (internal friction force). • ASFFi,t= Turbulent friction within the snow/air suspension, (air suspension friction force). • AFFi,t=Shear between the avalanche and the surrounding air, (air friction force). • FFFi,t= Fluid-dynamic drag at the front of the avalanche
GISRUK 2007 26
5
GISRUK 2007
27
5
GISRUK 2007
28
5
GISRUK 2007
29
1 vs 3
GISRUK 2007
30
Wildfire
The simulation of a wildfire using the BEHAVE model and GISSim techniques for the propagation. Some EVOSim techniques are used to represent the extinction model. (video).
All the elements can be defined using VRML or X3D languaje. The simulator uses a default library with the more common elements needed to repesent the simulation model.
In the next picture, a landscape is shown. This is the initial view of a model, representing the diferent layers that configures the variables. Usually a first layer with the DTM (Digital Terrain Model) is used as a base for all the other layers (vegetation, paths, rivers, etc). Since the model can define different types ofvegetation, different layers representing each one of these layers can be used in the simulation.
Once the model is configured, the simulation can be executed. A least one point is selected, as the origin of the fire. The simulation engine calculates the fire evolution representing the wildfire as can be viewed in the last picture.
This video shows the execution of a wildfire model.
Once the simulation finish the results can be represented in the virtual reality environment.
The virtual reality model is build using VRML with the Cortona browser embedded in the application.
GISRUK 2006
http://www.nottingham.ac.uk/geography/GISRUK/ 5-7h April 2006, University of Nottingham (UK) |
.jpg) |
GISRUK 2004
http://www.geo.ed.ac.uk/gisruk/gisruk.html 28-30h April 2004, University of East Anglia (Norwich) (UK) |
.jpg) |
Water
Three different researches I conduct regarding water.
Simulation of a river basin
One is related with the flow of the water in a defined environment, representing the river basins and other elements.

Sea level rise
The other research is related with the sea level rise in two different aspects, the representation, and the construction of a model to obtain the new level of the water. In the media section two videos showing the preliminary models are shown.
Black tide
The last research is related with the propagation of a black tide. In the figure is shown a propagation of petroleum over the sea surface using VRML language to represent the model.

Some media
| Here you can see the sea level rise model in the city of New York. The model elevates the water aproximately 100 meters (its not real, here we are testing the web browser infraestructure to represent the simulation model). | |
|
The same model in the city of Barcelona. |
Some publications
If you have a question about the publications please feel free to ask me anything.
ASM 2008
http://iasted.org/conferences/pastinfo-609.html June 23 – 25, 2008 Corfú (Grece) |
ASM 2008 Presentation
SDL FORMALIZATION OF A HYDROLOGIC MODEL
Jeaneth López C., Pau Fonseca i Casas, Josep Casanovas
Outline
§ § § § § § Hydrologic Models Simulation Formalisms GIS data Cellular automaton SDL Specification of the model. Discussion
Hydrologic Models
IPCC estimates that there are four places in the earth with high risk to reduce the availability of hydrologic resources and present abrupt climate changes. Spain (south of Europe), California (EEUU), South Africa, North east of
Greenhouse effects
Hydrologic resource
Rise Sea level Natural disastres
•Cyclones •Droughts •Floods •Frost •Etc…
Human Migration
Rise Temperature
Water Availability
Increase of population Precipi tation Contami nation Waste water
Human Consume Agricul ture
Available Water
Industry Ecosystems
Hydro. model – Sim. Formalisms – GIS Data – Cel. Automaton - SDL
Hydrologic Models
Watershed modeling, or hydrologic model (rainfall-runoff modeling) began in the 1950s and 1960s with the evolution of the digital computer. The Stanford Watershed Model (SWM) was one of the first watershed hydrologic model. (Crawford and Linsey 1966). LSSMs (Large-scale Spatial Models)(Watson et al., 1999) DHSVM (Distributed Hydrology-Soil-Vegetation Model) (Wigmosta 1997, 2002) LSHWM (Large-Scale Hybrid Watershed Modeling)(Aral and Gunduz, 2003), MHM (Macroscale Hydrological Model using Variable Infiltration Capacity VIC 3-layer)(Srinivasan2003) The VIC-3L model, is based on a 3-layer Soil Vegetation Atmosphere Transfer scheme to model different surface conditions. L-THIA (Long Term Hydrologic Impacts Assessment) (Lim et al., 2006) Hydrological model SHALL3 (Zimmermann, 2002) (Haan et al.,1982, Singh, 1988, Singh and Frevert, 2006)
Hydro. model – Sim. Formalisms – GIS Data – Cel. Automaton - SDL
Hydrologic Models
The SWAT (Soil and Water Assessment Tool) was developed by modifying the models specified below. All of this models use the SCS Curve Number Method, an empirical formula for predicting runoff from daily rainfall.
GLEAMS
pesticide compone nt daily rainfall hydrology component Crop Growth compone nt
QUAL2 E
Instream kinetics
Example SWAT adaptations
ESWAT SWATG SWIM
SWRRB
(multiple subbasins, subbasins, other other
CREAMS
SWRRB (multiple
SWAT
routing structur e
components)
EPIC
ROTO
Schematic of SWAT developmental history, including selected SWAT
1970s
Hydro. model – Sim. Formalisms – GIS Data – Cel. Automaton - SDL
Nowada ys
Simulation Formalisms
§ Petri Nets
§ Introduced by Carl Adam Petri (1960). Also known as a Place/Transition
§ DEVS (Discreet Event System Specification)
§ In the 70s Bernard Zeigler proposed a mathematical formalism.
§ SDL (Specification and Description Language)
§ The semantics of SDL was defined formally in 1988.
Hydro. model – Sim. Formalisms – GIS Data – Cel. Automaton - SDL
Petri Nets
RdP=(P,T,A,W,M0)
P = Finiteset of nodes Places T = Finiteset of nodes Transitions A C(PxT) and T. (TxP): subset of cartesianproduct between nodes P
W = a {1,2,3,..}: weigh of arcs M0 = Pi {1,2,3,..} node Pi: number ok tokens initials in each place
Hydro. model – Sim. Formalisms – GIS Data – Cel. Automaton - SDL
DEVS Formalism
M=<X, S, Y, δint, δext, λ, ta> where: X: set of input values. S: set of states values. Y: set of output values. δint: internal transition function.
δint :S
S
δext: external transition function. δext Q x X S , on
Q={(s,e)|sS, 0≤e≤ta(s)} set of states. e elapsed time from the last transition.
λ : output function: λ : S Y ta : time advance function.
ta: S
R+0∞
DEVS Processor example
M=<X, S, Y, δint, δext, λ, ta> on: X={job1, job2, .., jobn} S={job1, job2,.., jobn}U[Ø]xR+0∞ Y={y(job1), y(job2),.. Y(jobn)} δint(job,σ)=(Ø, ∞) δext(job,σ,e,x)= if job= Ø (x,tp,(x)) else (job, σ-e) λ(job, σ)=y(job) Ta(job, σ)= σ
SDL formalism
Object-oriented, formal language defined by The International Telecommunications Union as recommendation Z.100. Intended for the specification of complex, event-driven, real-time, and interactive applications involving many concurrent activities that communicate using discrete signals.
Hydro. model – Sim. Formalisms – GIS Data – Cel. Automaton - SDL
SDL Formalism
The semantics of SDL was defined formally in 1988.
Standard Formal Graphical
and symbol-based Object-oriented (OO)
Hydro. model – Sim. Formalisms – GIS Data – Cel. Automaton - SDL
GIS Data
Hydro. model – Sim. Formalisms – GIS Data – Cel. Automaton - SDL
Celular automaton
Each cell xi(t) represent a state of the cell i in the instant t. k = {Empty, Static and Dynamic}
xi
Hydro. model – Sim. Formalisms – GIS Data – Cel. Automaton - SDL
Game of life
The Game of Life is a cellular automaton devised by the British mathematician John Horton Conway in 1970. It is the best-known example of a cellular
Hydro. model – Sim. Formalisms – GIS Data – Cel. Automaton - SDL
Method
§ Cellular Automaton Structure
§ Evolution Rules
§ Precipitation phase § Settlement phase
• Data layers
Hydro. model – Sim. Formalisms – GIS Data – Cel. Automaton - SDL
Model
Soil (Ground)
•Return Flow •Kind of soil •Saturate •Kind of soil use •Non-Saturate •Percolation
•Runoff •Humidity •Evapo-trans piration •Temperature •Rainfall •Precipitation
Hydrologic resource
Meteorology
Factors/variables which affects hydrologic resource
Hydro. model – Sim. Formalisms – GIS Data – Cel. Automaton - SDL
Model
Where:
SWt is the total quantity of water in the soil (basin) (mm), SWi is the initial quantity of water in the soil (mm) Ri (rainfall) is the quantity of rain in the period of analysis(mm) Qi is the quantity of runoff (mm) ETi is the evapotranspiration (mm) Pi is the percolation (mm) QRi return flow(mm) t is the time expressed in days i is the index of cell
Hydro. model – Sim. Formalisms – GIS Data – Cel. Automaton - SDL
Model
This expression gives us the water volume existing in each cell of our cellular automaton in a specific time t. In the expression, one position of the cellular automaton matrix [xi,xj] is represented by the cell xi.
Hydro. model – Sim. Formalisms – GIS Data – Cel. Automaton - SDL
System diagram
Hydro. model – Sim. Formalisms – GIS Data – Cel. Automaton - SDL
States diagram
Update Receive
Send
Dynamic
Receiv e
Static
d en S te/ ei ec R ve
Update Receive
Receive
Send
Up
da
Send Update
Empty
Hydro. model – Sim. Formalisms – GIS Data – Cel. Automaton - SDL
Process diagram: Static state
Hydro. model – Sim. Formalisms – GIS Data – Cel. Automaton - SDL
Process diagram: Empty state
Hydro. model – Sim. Formalisms – GIS Data – Cel. Automaton - SDL
Process diagram: Dynamic state
Hydro. model – Sim. Formalisms – GIS Data – Cel. Automaton - SDL
Discussion and future work
This slides depicts the first and more important step to construct a discrete hydrologic simulator based in a cellular automaton. It shows the specification of hydrologic model with the aim of simulate the behaviour of water in a river basin. The use of the cellular simplifies the mathematical expressions and helps us to maintain a structured view of the geographical data needed to represent the model. The use of SDL formalism simplifies the understanding of the behaviour of model thanks its graphical structure. The model is based in the hydrologic balance equation which permits calculate the quantity exist in each cell of the cellular automaton
Hydro. model – Sim. Formalisms – GIS Data – Cel. Automaton - SDL
References
[1] L. Ma, L.R. Ahuja, and R.W. Malone. Systems Modeling for Soil and Water Research and Management: Current Status and Needs for the 21st Century. ASABE, 1907-2007. [2] IPCC Intergovernamental Panel on Climate Change. Report IPCC. 2007. [3] J. Samper, M.A. Garcia, B. Pisani, D. Alvares, A. Varela, and J.A. Losada. Modelos Hidrologicos y Sistemas de Informacion Geografica para la Estimacion de Recursos Hidricos:. Confederacin Hidrologica del Ebro, VII, 2005. [4] E. Guzman, J. Bonini, and D. Matamoros. Modelo Hidrologico SWAT (Soil Water Assessment Tool) Prediccin de Caudales y Sedimentos en una Cuenca. Revista Tecnologica, 17:152–161, 2004. [5] Erik D. Zimmermann. Modelo Hidrologico Superficial y Subterraneo. Centro Universitario rosario de Investigaciones Hidroambientales. [6] A. López, D. Sauri, and Jose M. Galán. Urban Water
References
[8] P. Pea and J. Alirio. Sobre las redes de petri r-difusas. Divulgaciones Matemticas, 7:87–99, 1999. [9] Gabriel Wainer. Applying cell-devs methodology for modeling the environment. SIMULATION, 82:635, 2006. [10] Liu Qi and Gabriel Wainer. Parallel environment for devs and cell-devs models. SIMULATION, 83:449, 2007. [11] Fonseca P. and Casanovas J. 2005. ESS205, Simplifying GIS data use inside discrete event simulation model through m_n-AC cellular automaton; Proceedings ESS 2005. [12] ITU-T Telecommunication Standardization Sector of ITU. Languages and general software aspects for telecommunication systems. TELECOMMUNICATION STANDARDIZATION SECTOR OF ITU, 2007. [13] Zeigler, B. P.; H. Praehofer; D. Kim. 2000. Theory of Modeling and Simulation. Academic Press. [14] Petri, Carl A. 1962. "Kommunikation mit Automaten". Ph. D. Thesis. University of Bonn. [15] Recalde, L.; Teruel, E.; Silva, M. 1999. Autonomous
Thanks!
Pau Fonseca i Casas pau@fib.upc.edu
Technical University of Catalonia Barcelona School of Informatics Computing laboratory Barcelona Jordi Girona 1-3 (+34)93401773
The financial market experiment
We present an experiment that aims to simulate the figure of the broker, from the point of view of human behavior adding hunches and expectations too its decisions. As a starting point we use the paper of Veiga and Vorsatz, "Price manipulation in an experimental asset market”, a study that analyzes the influence on the behavior the other brokers due to an agent handle and a trading robot that performs with the intention of distort the market and thus, try to profit from their operations. In this research conducted by Veiga and Vorsatz, it is required the participation of real people whit the aim of analyze the behavior of the process of buying and selling a value in two separate rooms, one with the influence of manipulative agent and another without it. This article reproduces this experiment but using virtual brokers that belongs to a multi-agent simulation model. The main objective is to reproduce the experiment represented in the Veiga and Vorsatz paper using intelligent agents detailing the description of the psychological behavior of the brokers.
To execute the models you must download the zip files, extract it on a folder and execute the SDLPS engine. The file that rules the behavior of the model is SimBroker.sdlps. This file contains all the details of both models.
Remember that SDLPS can only be used to execute the models or for academic purposes. (POSAR LA LLICÈNCIA FORMAT UPC).
| Attachment | Size |
|---|---|
| Low hunches model | 26.62 MB |
| SDLPS simulator | 31.04 MB |