Consider adding a constraint to a problem after solving it. Imagine that you want to optimize a linear program:

Primal:

Dual:

max

-x1

+

x2

+

x3

min

6y1

+

5y2

st

x1

+

x2

+

2x3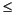

6

st

y1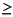

-1

x2

+

x3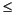

5

y1

+

y2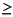

1

0

2y1

+

y2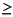

1

x1,

x2,

x3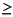

0

y1,

y2,

y3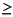

0

Note that the first constraint in the dual (y1 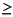-1) is redundant. Presolve can use this information about the dual problem (and complementary slackness) to conclude that variable x1 can be fixed to 0 and removed from the presolved problem. While it may be intuitively obvious from inspection of the primal problem that x1 can be fixed to 0, it is important to note that dual information (redundancy of the first dual constraint) is used to prove it formally.

Now consider the addition of a new constraint x2 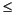5x1:

Primal:

Dual:

max

-x1

+

x2

+

x3

min

6y1

+

5y2

st

x1

+

x2

+

2x3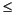

6

st

y1

-

5y3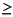

-1

x2

+

x3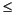

5

y1

+

y2

+

y3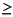

1

- 5x1

+

x2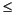

0

2y1

+

y2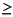

1

x1,

x2,

x3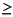

0

y1,

y2,

y3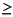

0

Our goal is to add the appropriate constraint to the presolved problem and reoptimize. Note, however, that the dual information presolve used to fix x1 to 0 was changed by the addition of the new constraint. The first constraint in the dual is no longer guaranteed to be redundant, so the original fixing is no longer valid (the optimal solution is now x1=1, x2=5, x3=0). As a result, CPLEX is unable to use the presolved problem to reoptimize.