Representing the Piecewise Linear Cost Function

INDEX PREVIOUS NEXT

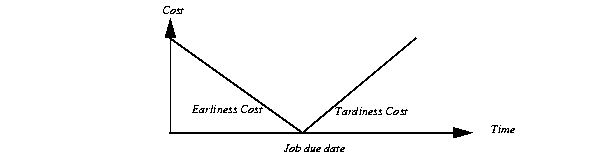
The earliness-tardiness cost function is the sum of piecewise linear functions having two segments, as you see in Figure 22.1. The function takes as an argument the completion date of the last activity of a job (in other words, the starting date plus the duration). In that two-segment function, the slope of the first segment is (-1) times the earliness cost, and the slope of the second segment is the tardiness cost. Moreover, at the due date, the cost is zero. Consequently, the function can be represented as a piecewise linear function with one breakpoint and two slopes, like this:

IloInt last = nbResource - 1;
IloExpr costSum(env);
for(j = 0; j < nbJob; j++) {
 costSum += IloPiecewiseLinear(s[j][last] + duration[j][last],
            IloNumArray(env, 1, jobDueDate[j]),
               IloNumArray(env, 2, -jobEarlinessCost[j], jobTardinessCost[j]),
            jobDueDate[j], 0);
 }
model.add(IloMinimize(env, costSum));