| Getting Started with MATLAB | Help Desk |
Scripts and Functions
MATLAB is a powerful programming language as well as an interactive computational environment. Files that contain code in the MATLAB language are called M-files. You create M-files using a text editor, then use them as you would any other MATLAB function or command. There are two kinds of M-files:myfunction.m, use
type myfunctionWhen you invoke a script, MATLAB simply executes the commands found in the file. Scripts can operate on existing data in the workspace, or they can create new data on which to operate. Although scripts do not return output arguments, any variables that they create remain in the workspace, to be used in subsequent computations. In addition, scripts can produce graphical output using functions like
plot.
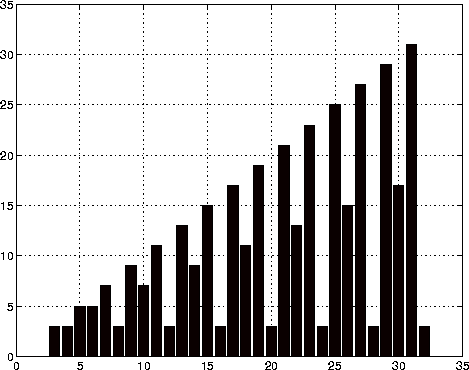
For example, create a file called magicrank.m that contains these MATLAB commands:
% Investigate the rank of magic squares r = zeros(1,32); for n = 3:32 r(n) = rank(magic(n)); end r bar(r)
 Typing the statement
Typing the statement
magicrankcauses MATLAB to execute the commands, compute the rank of the first 30 magic squares, and plot a bar graph of the result. After execution of the file is complete, the variables
n and r remain in the workspace.
Functions are M-files that can accept input arguments and return output arguments. The name of the M-file and of the function should be the same. Functions operate on variables within their own workspace, separate from the workspace you access at the MATLAB command prompt.
A good example is provided by rank. The M-file rank.m is available in the directory
toolbox/matlab/matfunYou can see the file with
type rankHere is the file.
function r = rank(A,tol) % RANK Matrix rank. % RANK(A) provides an estimate of the number of linearly % independent rows or columns of a matrix A. % RANK(A,tol) is the number of singular values of A % that are larger than tol. % RANK(A) uses the default tol = max(size(A)) * norm(A) * eps. s = svd(A); if nargin==1 tol = max(size(A)) * max(s) * eps; end r = sum(s > tol);The first line of a function M-file starts with the keyword
function. It gives the function name and order of arguments. In this case, there are up to two input arguments and one output argument.
The next several lines, up to the first blank or executable line, are comment lines that provide the help text. These lines are printed when you type
help rankThe first line of the help text is the H1 line, which MATLAB displays when you use the
lookfor command or request help on a directory.
The rest of the file is the executable MATLAB code defining the function. The variable s introduced in the body of the function, as well as the variables on the first line, r, A and tol, are all local to the function; they are separate from any variables in the MATLAB workspace.
This example illustrates one aspect of MATLAB functions that is not ordinarily found in other programming languages - a variable number of arguments. The rank function can be used in several different ways:
rank(A) r = rank(A) r = rank(A,1.e-6)Many M-files work this way. If no output argument is supplied, the result is stored in
ans. If the second input argument is not supplied, the function computes a default value. Within the body of the function, two quantities named nargin and nargout are available which tell you the number of input and output arguments involved in each particular use of the function. The rank function uses nargin, but does not need to use nargout.
If you want more than one function to share a single copy of a variable, simply declare the variable as global in all the functions. Do the same thing at the command line if you want the base workspace to access the variable. The global declaration must occur before the variable is actually used in a function. Although it is not required, using capital letters for the names of global variables helps distinguish them from other variables. For example, create an M-file called falling.m:
function h = falling(t) global GRAVITY h = 1/2*GRAVITY*t.^2;Then interactively enter the statements:
global GRAVITY GRAVITY = 32; y = falling((0:.1:5)');The two global statements make the value assigned to
GRAVITY at the command prompt available inside the function. You can then modify GRAVITY interactively and obtain new solutions without editing any files.
MATLAB commands are statements like
load helpMany commands accept modifiers that specify operands.
load August17.dat help magic type rankAn alternate method of supplying the command modifiers makes them string arguments of functions.
load('August17.dat')
help('magic')
type('rank')
This is MATLAB's "command/function duality." Any command of the form
command argumentcan also be written in the functional form
command('argument')
August1.dat, August2.dat, and so on. It uses the function int2str, which converts an integer to a character string, to help build the file name.
for d = 1:31 s = ['August' int2str(n) '.dat'] load(s) % Process the contents of the d-th file endThe
eval function works with text variables to implement a powerful text macro facility. The expression or statement
eval(s)uses the MATLAB interpreter to evaluate the expression or execute the statement contained in the text string
s.
The example of the previous section could also be done with the following code, although this would be somewhat less efficient because it involves the full interpreter, not just a function call.
for d = 1:31 s = ['load August' int2char(n) '.dat'] eval(s) % Process the contents of the d-th file endTo obtain the most speed out of MATLAB, it's important to vectorize the algorithms in your M-files. Where other programming languages might use
for or DO loops, MATLAB can use vector or matrix operations. A simple example involves creating a table of logarithms.
x = 0; for k = 1:1001 y(k) = log10(x); x = x + .01; end
x = 0:.01:10; y = log10(x);For more complicated code, vectorization options are not always so obvious. When speed is important, however, you should always look for ways to vectorize your algorithms. If you can't vectorize a piece of code, you can make your
for loops go faster by preallocating any vectors or arrays in which output results are stored. For example, this code uses the function zeros to preallocate the vector created in the for loop. This makes the for loop execute significantly faster.
r = zeros(32,1);
for n = 1:32
r(n) = rank(magic(n));
end
Without the preallocation in the previous example, the MATLAB interpreter enlarges the r vector by one element each time through the loop. Vector preallocation eliminates this step and results in faster execution.
A class of functions, called "function functions," works with nonlinear functions of a scalar variable. That is, one function works on another function. The function functions include
humps from the matlab/demos directory:
function y = humps(x) y = 1./((x-.3.^2 + .01) + 1./((x-.9).^2 + .04) - 6;Evaluate this function at a set of points in the interval 0
 x
x  1 with
1 with
x = 0:.002:1; y = humps(x);Then plot the function with
plot(x,y)
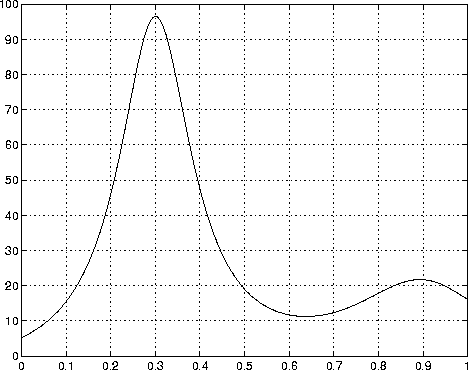 The graph shows that the function has a local minimum near x = 0.6. The function
The graph shows that the function has a local minimum near x = 0.6. The function fmins finds the minimizer, the value of x where the function takes on this minimum. The first argument to fmins is the name of the function being minimized and the second argument is a rough guess at the location of the minimum.
p = fmins('humps',.5)
p =
0.6370
To evaluate the function at the minimizer,
humps(p) ans = 11.2528Numerical analysts use the terms quadrature and integration to distinguish between numerical approximation of definite integrals and numerical integration of ordinary differential equations. MATLAB's quadrature routines are
quad and quad8. The statement
Q = quad8('humps',0,1)
computes the area under the curve in the graph and produces
Q = 29.8583Finally, the graph shows that the function is never zero on this interval. So, if you search for a zero with
z = fzero('humps',.5)
you will find one outside of the interval
z = -0.1316